Key Terms:
Factoring: a process by which more complicated expressions are rewritten as the product of simpler expressions.
Fundamental Theorem of Algebra: any polynomial of degree n will have n roots (including complex numbers)
Parabola: the graph of a quadratic function.
Polynomial: an algebraic expression that can contain constants, variables, and exponents that are combined using addition, subtraction, and multiplication. Polynomials can be named by the number of terms that they have: one term is a monomial, two terms is a binomial, and three terms is a trinomial.
Quadratic Equation: a polynomial equation in which the highest exponent, or degree, is two (2).
Roots of a Quadratic Equation: also called the zeros; these are the solutions to a quadratic equation. These are also the x-intercepts of its graph.
x-intercept: a point, or ordered pair (x, y), where the graph of a relation intersects with the x-axis. The y-value of this point will always be zero (0).
Key Formulas:
The Quadratic Formula
If ax^2 bx c=0, then x= (-b±√(b^2-4ac))/2a
When solving quadratic equations involving three terms, you will inevitably find equations that are not factorable. In this case, you will not be able to use the Zero-Product Property to solve them. So, if you cannot factor the quadratic, how do you solve for the variable? You use a formula called the Quadratic Formula!
I should take a moment to mention that the quadratic formula will solve every quadratic equation for you; however, it is typically much more time consuming if you are able to factor instead. That being said, it is a powerful tool with which you want to become very familiar.
Let’s take a look at this example problem. Solve for x: 12x^2=5 10xOur first step will be to put the quadratic equation in standard form and set it equal to zero. We can do that by subtracting 5 and 10x from both sides.
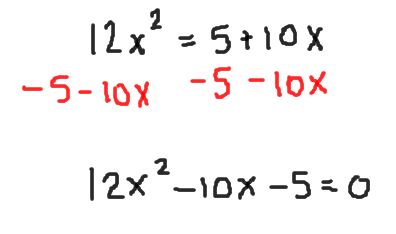
If you tried to factor this expression, you would find that it does not factor. So, we need to use the Quadratic Formula. The Quadratic Formula states that the solutions to any quadratic equation can be found as long as the equation is written in standard form ax^2 bx c=0. You simply plug-in the values for a, b, and c. Here, a = 12, b = -10, and c = -5.
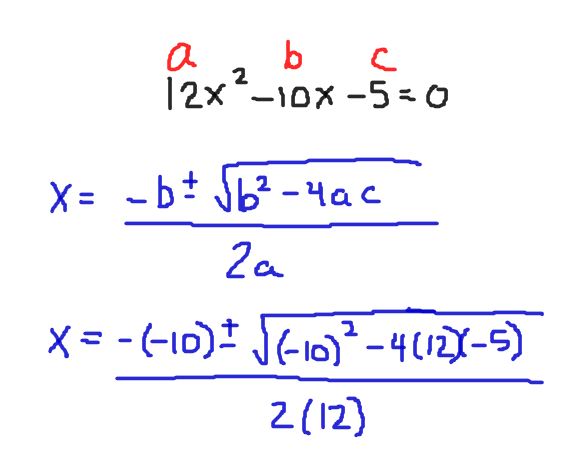
Now that you have all of the terms written in the equation, you keep simplifying until you reach your final answers. Remember, a quadratic equation will have at most two real solutions.
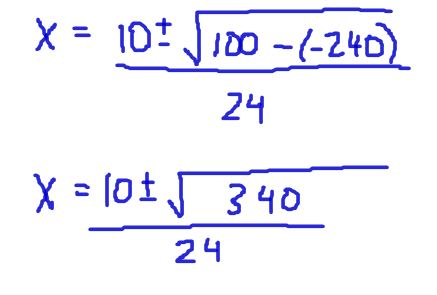
At this point, you have two solutions because of the ± sign that is in the problem. This sign is read as “plus or minus” and it means:

You now have two options for final answers. If you are asked for approximate answers, you can type each of the expressions into a calculator and find that:


However, most often, you will be asked for exact answers. If that is the case, then you are going to need to be able to simplify the square root by knowing that √340=2√85. Here is the way to write the exact answers.
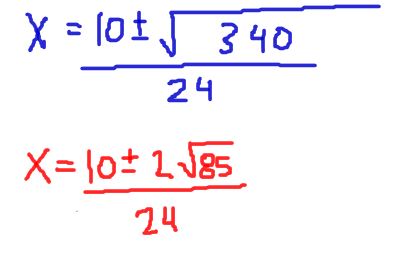
Notice that each of the terms outside of the radical are divisible by 2, and so we can simplify one step further to:
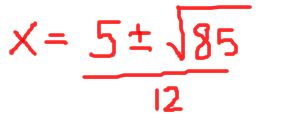
And that gives us two exact answers of:
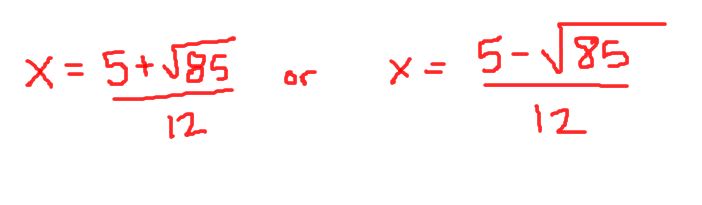
As a side note, if you typed both of those answers into a calculator, you would get the same approximate decimal answers that we got earlier in the problem. You can always check your work that way.